Платоновы тела
Платоновы тела
Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук.
Л. Кэррол
Человек всегда проявлял интерес к многогранникам. Некоторые из правильных и полуправильных тел встречаются в природе в виде кристаллов, другие – в виде вирусов, которые можно рассмотреть с помощью электронного микроскопа. Что же такое многогранник? Многогранником называется часть пространства, ограниченная совокупностью конечного числа плоских многоугольников.
Издавна ученые интересовались «идеальными» или правильными многоугольниками, то есть многоугольниками, имеющими равные стороны и равные углы. Простейшим правильным многоугольником можно считать равносторонний треугольник, поскольку он имеет наименьшее число сторон, которое может ограничить часть плоскости. Общую картину интересующих нас правильных многоугольников наряду с равносторонним треугольником составляют: квадрат (четыре стороны), пентагон (пять сторон), гексагон (шесть сторон), октагон (восемь сторон), декагон (десять сторон) и т. д. Очевидно, что теоретически нет каких-либо ограничений на число сторон правильного многоугольника, то есть число правильных многоугольников бесконечно.
Что же такое правильный многогранник? Правильным называется такой многогранник, все грани которого равны (или конгруэнтны) между собой и при этом являются правильными многоугольниками. Сколько же существует правильных многогранников? В XIII книге «Началах Эвклида», посвященной правильным многогранникам, или платоновым телам (Платон их рассматривает в диалоге «Тимей») мы находим строгое доказательство того, что существует только пять правильных многогранников, а их гранями могут быть только три типа правильных многоугольников: треугольники, квадраты и пентагоны.
Доказательство того, что существует ровно пять правильных выпуклых многогранников, очень простое.
Очевидно, что каждая вершина многогранника может принадлежать трем и более граням. Сначала рассмотрим случай, когда грани многогранника – равносторонние треугольники. Поскольку внутренний угол равностороннего треугольника равен 60°, три таких угла, помещенные на плоскость, дадут в сумме 180°. Если теперь согнуть эти углы по внутренним сторонам и склеить по внешним, получим многогранный угол тетраэдра – правильного многогранника, в каждой вершине которого встречаются три правильные треугольные грани. Три правильных треугольника с общей вершиной называется разверткой вершины тетраэдра. Если добавить к развертке вершины еще один треугольник, в сумме получится 240°. Это развертка вершины октаэдра. Добавление пятого треугольника даст угол 300° – мы получаем развертку вершины икосаэдра. Если же добавить еще один, шестой треугольник, сумма углов станет равной 360° – эта развертка, очевидно, не может соответствовать ни одному выпуклому многограннику.
Теперь перейдем к квадратным граням. Развертка из трех квадратных граней имеет угол 3 x 90° = 270° – получается вершина куба, который также называют гексаэдром. Добавление еще одного квадрата увеличит угол до 360° – этой развертке уже не соответствует никакой выпуклый многогранник.
Три пятиугольные грани дают угол развертки 3 x 108° = 324° – вершина додекаэдра. Если добавить еще один пятиугольник, получим больше 360°.
Для шестиугольников уже три грани дают угол развертки 3 x 120° = 360°, поэтому правильного выпуклого многогранника с шестиугольными гранями не существует. Если же грань имеет еще больше углов, то развертка будет иметь еще больший угол. Значит, правильных выпуклых многогранников с гранями, имеющими шесть и более углов, не существует.
Таким образом, мы убедились, что существует лишь пять выпуклых правильных многогранников – тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями.
Пять правильных многогранников или платоновых тел использовались и были известны задолго до времени Платона. Кейт Кричлоу в своей книге «Время остановилось» дает убедительное свидетельство тому, что они были известны людям неолита Британии, по крайней мере, за 1000 лет до Платона. Это заявление основывается на наличии ряда сферических камней, хранящихся в музее Ашмолина в Оксфорде. Эти камни, размеры которых соответствовали тому, что можно уместить в руке, были покрыты геометрически точными сферическими фигурами куба, тетраэдра, октаэдра, икосаэдра и додекаэдра, также как и некоторые дополнительные сложносоставные и псевдоправильные тела, такие как кубо-октаэдр и ико-додекаэдр. Кричлоу говорит: «То что у нас есть, представляет собой объекты, несомненно указывающие на степень математических способностей, которые до сих пор отрицались в отношении человека неолита некоторыми археологами или историками математики».
Теэтет Афинский (417–369 до н. э.), современник Платона, дал математическое описание правильных многогранников и первое известное доказательство того, что их ровно пять.
В «Тимее», который, по сравнению со всеми остальными работами Платона, носит наиболее ярко выраженный пифагорейский характер, он утверждает, что четырьмя базовыми элементами в мире являются земля, воздух, огонь и вода, и что каждый из этих элементов соотносится с одной из пространственных фигур. Традиция связывает куб с землей, тетраэдр с огнем, октаэдр с воздухом и икосаэдр с водой. Платон упоминает «некое пятое построение», использованное создателем при сотворении вселенной. Так додекаэдр стал ассоциироваться с пятым элементом: эфиром. Устроитель вселенной Платона установил порядок из первобытного хаоса этих элементов с помощью основополагающих форм и чисел. Приведение в порядок в соответствии с числом и формой на более высоком уровне привело к предначертанному расположению пяти элементов в физической вселенной. Основополагающие формы и числа затем стали действовать в качестве границы раздела между высшим и низшим мирами. Сами по себе и в силу своей аналогии с другими элементами, они обладали способностью формировать материальный мир.
Те же пять правильных тел в соответствии с классической традицией рисуются таким образом, что они содержатся в девяти концентрических шарах, и каждое тело соприкасается со сферой, которая описана вокруг следующего тела, расположенного внутри ее. Такая композиция проявляет немало важных взаимоотношений и заимствована из дисциплины, называемой corpo transparente, относящейся к восприятию сфер, изготовленных из прозрачного материала и размещенных одна в другой. Такое наставление давалось Фра Лукой Паччоли многим великим людям Ренессанса, включая Леонардо и Брунуллески.
В своей книге «Тайна мира» (Mysterium Cosmographicum), которая вышла в свет в 1596 г. Иоганн Кеплер предположил, что существует связь между пятью платоновыми телами и шестью открытыми к тому времени планетами Солнечной системы. Согласно этому предположению, в сферу орбиты Сатурна можно вписать куб, в который вписывается сфера орбиты Юпитера. В нее, в свою очередь, вписывается тетраэдр, описанный около сферы орбиты Марса. В сферу орбиты Марса вписывается додекаэдр, в который вписывается сфера орбиты Земли. А она описана около икосаэдра, в который вписана сфера орбиты Венеры. Сфера этой планеты описана около октаэдра, в который вписывается сфера Меркурия. Такая модель Солнечной системы получила название «Космического кубка» Кеплера. Расхождение между моделью Кеплера и реальными размерами орбит (порядка нескольких процентов) И. Кеплер объяснял «влиянием материи».
В XX веке платоновы тела были использованы в теории electron shell model Роберта Муна, которая также известна как «теория Муна». Мун заметил, что геометрическое расположение протонов и нейтронов в атомном ядре связано с положением вершин вложенных платоновых тел. Эта концепция была вдохновлена работой И. Кеплера «Mysterium Cosmographicum».
Существует формула Эйлера для многогранников:
F + V = E + 2
В этой формуле F – число граней, V – число вершин, E – число ребер. Эти числовые характеристики для платоновых тел приведены в таблице.
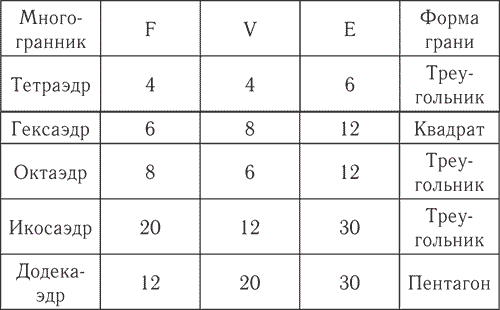
Количественные особенности платоновых тел
Важные соотношения между ребрами, диаметрами вписанных и описанных сфер, площадями и объемами правильных многогранников выражаются через иррациональные числа. В таблице ниже представлено отношение длины ребра к диаметру описанной сферы для каждого из пяти платоновых тел.
Каждый полученный результат есть иррациональное число, которое можно найти только через извлечение квадратного корня. Мы видим, что здесь фигурируют числа, которые являются важными и особенными в сакральной математике.
Геометрия додекаэдра и икосаэдра связана с золотой пропорцией. Действительно, гранями додекаэдра являются пентагоны, т. е. правильные пятиугольники, основанные на золотой пропорции. Если внимательно посмотреть на икосаэдр, то можно увидеть, что в каждой вершине икосаэдра сходится пять треугольников, внешние стороны которых образуют пентагон. Уже этих фактов достаточно, чтобы убедиться в том, что золотая пропорция играет существенную роль в конструкции этих двух платоновых тел. Эти две фигуры являются обратными друг другу: обе состоят из 30 ребер, но, несмотря на это, икосаэдр имеет 20 граней и 12 вершин, а додекаэдр – 12 граней и 20 вершин. Также обратными друг другу являются октаэдр и гексаэдр, и театраэдр сам к себе.
Существуют удивительные геометрические связи между всеми правильными многогранниками. Так, например, куб и октаэдр дуальны, т. е. получаются друг из друга, если центры тяжести граней одного принять за вершины другого и обратно. Аналогично дуальны икосаэдр и додекаэдр. Тетраэдр дуален сам себе. Додекаэдр получается из куба построением «крыш» на его гранях (способ Евклида), вершинами тетраэдра являются любые четыре вершины куба, попарно не смежные по ребру, то есть из куба могут быть получены все остальные правильные многогранники.
Роберт Лолор в своей работе показывает, что платоновы тела можно построить исходя из икосаэдра. Он пишет: «Если мы соединим все внутренние вершины икосаэдра, нарисовав три линии из каждой из них, соединяющих каждую вершину с ей противолежащей, и затем из двух верхних вершин проведем четыре линии к двум противоположным, так чтобы эти линии сошлись в центре, мы, действуя в соответствии со сказанным, естественным образом построим ребра додекаэдра. Такое построение происходит автоматически при пересечении внутренних линий икосаэдра. После создания додекаэдра мы можем, просто используя шесть из его вершин и центр, построить куб. Используя диагонали куба, мы можем построить звездообразный или переплетенный тетраэдр. Пересечения звездообразного тетраэдра с кубом дают нам точное местоположение для построения вписанного октаэдра. Затем в самом октаэдре с использованием внутренних линий икосаэдра и вершин октаэдра получается второй икосаэдр. Мы прошли через весь полный цикл, пять этапов от семени к семени. И такие действия представляют собой бесконечную последовательность.
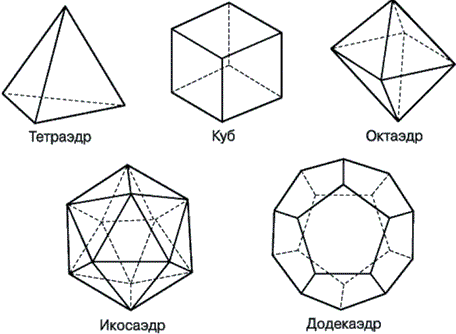
Тетраэдр
Простейшим среди правильных многогранников является тетраэдр. У Платона он соответствует стихии Огня. В физике «огонь» можно соотнести с состоянием плазмы. Тетраэдр имеет наименьшее число граней среди Платоновых тел и является трехмерным аналогом плоского правильного треугольника, который имеет наименьшее число сторон среди правильных многоугольников. Его четыре грани – равносторонние треугольники. Четыре – это наименьшее число граней, отделяющих часть трехмерного пространства. Каждая его вершина является вершиной трех треугольников. Все многогранные углы тетраэдра равны между собой. Сумма плоских углов при каждой вершине равна 180°. Таким образом, тетраэдр имеет 4 грани, 4 вершины и 6 ребер.
Октаэдр
Октаэдр составлен из восьми равносторонних треугольников. У Платона он соответствует стихии Воздуха. В физике «воздух» можно соотнести с газообразным состоянием вещества. Каждая его вершина является вершиной четырех треугольников. Противоположные грани лежат в параллельных плоскостях. Сумма плоских углов при каждой вершине равна 240°. Таким образом, октаэдр имеет 8 граней, 6 вершин и 12 ребер.
Икосаэдр
Икосаэдр – одно из пяти платоновых тел, по простоте следующее за тетраэдром и октаэдром. У Платона он соответствует стихии Воды. В физике «воду» можно соотнести с жидким состоянием вещества. Икосаэдр составлен из двадцати равносторонних треугольников. Каждая его вершина является вершиной пяти треугольников. Сумма плоских углов при каждой вершине равна 300°. Таким образом, икосаэдр имеет 20 граней, 12 вершин и 30 ребер.
Гексаэдр
Гексаэдр или куб составлен из шести квадратов. У Платона он соответствует стихии Земли. В физике «землю» можно соотнести с твёрдым состоянием вещества. Каждая его вершина является вершиной трех квадратов. Сумма плоских углов при каждой вершине равна 270°. Таким образом, куб имеет 6 граней, 8 вершин и 12 ребер.
Додекаэдр
Додекаэдр составлен из двенадцати равносторонних пятиугольников. У Платона он соответствует пятому элементу – Эфиру. Каждая его вершина является вершиной трех пятиугольников. Сумма плоских углов при каждой вершине равна 324°. Таким образом, додекаэдр имеет 12 граней, 20 вершин и 30 ребер.
Правильные многогранники встречаются в живой природе. В начале XX века Эрнст Геккель (Ernst Haeckel) описал ряд организмов, формы скелета которых подобны различным правильным многогранникам. Например: Circoporus octahedrus, Circogonia icosahedra, Lithocubus geometricus и Circorrhegma dodecahedra. Формы скелета этих организмов запечатлены в их названиях.
Скелет одноклеточного организма феодарии (Circogoniaicosahedra) по форме напоминает икосаэдр. Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное пытается себя защитить: из 12 вершин скелета выходят 12 полых игл. На концах игл находятся зубцы, делающие иглу еще более эффективной при защите.
Многие вирусы, например вирус herpes, имеют форму правильного икосаэдра. Вирусные структуры строятся из повторяемых протеиновых субъединиц, и икосаэдр – самая подходящая форма для воспроизведения этих структур.
Кристаллические решётки многих минералов имеет форму платоновых тел.
Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана (FeS). Кристаллы этого химического вещества имеют форму додекаэдра. Минерал сильвин имеет кристаллическую решетку в форме куба. Кристаллы пирита имеют форму додекаэдра, а куприт образует кристаллы в форме октаэдров.
Платоновы тела – очень важный объект для изучения, как с точки зрения сакральной математики, так и с точки зрения естественных наук. Платоновы тела проявляются повсюду, начиная от вирусов, многие из которых имеют икосаэдрическую форму и заканчивая сложными макроструктурами, такими, например, как Солнечная система.
Антон Мухин
Данный текст является ознакомительным фрагментом.